For most students, math tends to be one of the more difficult subjects in school. Even for those who enjoy math, however, trigonometry can be a significant challenge. But with the right approach, anyone can break trigonometry down into simple, easily understood ideas. This guide will teach you the basics of trigonometry and give clear explanations and examples to help you understand the subject and overcome any struggles you may be experiencing.
Don't struggle with math alone! Let Learner's expert online tutors guide you to success. With our deep understanding of math and years of experience helping students just like you, we can help you conquer even the toughest math challenges.
Math Tutors for Trigonometry
Struggling with trigonometry is very common. Even compared to other types of math, this area can be complicated to fully understand. With a tutor’s help, however, you might be surprised at how easy it can be.
Unlike studying alone, a good trigonometry tutor can provide systematic methods for approaching trigonometry questions and understanding the concepts at work. Across multiple sessions, these experts can walk you through each step and identify techniques that work best for your learning style.
At Learner, our math tutors can explain everything you need to know about trigonometry. We recognize that mastery of the subject is both valuable and difficult to obtain, which is why we recommend beginning tutoring sessions early on during the course of your studies.
Though it may have frustrated you in the past, trigonometry doesn't have to be confusing. With the help of a math tutor, you can gain a deeper understanding of the subject, develop stronger problem-solving skills, improve your grades, and boost your self-confidence.
What is Trigonometry?
Trigonometry is a type of math that deals with triangles, their sides and angle measurements, and how these measurements relate to one another. The word trigonometry comes from the Greek words trigonon and metron, meaning “triangle” and "measure,” respectively.
Many students wonder why they would ever need to understand triangles so deeply. In reality, many careers require and use trigonometry, such as those of physicists, astronauts, surveyors, crime scene investigators, architects, engineers, and more.
Aside from career-specific use, trigonometrical concepts are also necessary to work out measurements of certain objects or spaces that are difficult to measure directly, such as the quantity of water in a lake or the heights of mountains. Trigonometry is also used in video game development to ensure that objects can move, and in music, it can measure the level or pitch of a sound wave.
Aside from its many applications, trigonometry is part of a well-formed and well-rounded general knowledge. Even if you don’t intend to pursue a career involving math, however, a poor grade in a required class such as trigonometry can seriously impact your overall academic record.
If you’re interested and would like to know more, learn exactly what trigonometry is.
The Basics of Trigonometry
Trigonometry is all about right-angled triangles, or triangles in which one internal angle measures 90°. Trigonometry acts as a system that allows you to calculate missing or unknown measurements of such a triangle, like the length of its sides or its angles.
A right-angled triangle has a single right angle. As a result, all of its sides have different lengths.
Take the Math Tutor Matching Quiz to Find the Best Trigonometry Tutor
The Components of a Right-Angled Triangle
A right-angled triangle is made up of several components, and we use specific terms to refer to these. They are as follows:
- 90° angle: Also called a right angle, this measurement is indicated by a small square in one corner of the triangle.
- Hypotenuse: The longest side of the right triangle opposite, which is always opposite the right angle.
- Opposite: Of the two sides which make up the right angle, the opposite is the vertical one.
- Adjacent: Of the two sides which make up the right angle, the adjacent is the horizontal one.
- Angle Theta: One of the two angles within a right triangle that are not right angles. This measurement may also be known as an “unknown angle” and is represented by the Greek symbol theta (θ)
Now that we’ve covered the main terms and components of right-angled triangles, let’s move on to one of trigonometry’s most common formulas: Pythagoras’ Theorem.
Pythagoras’ Theorem
Pythagoras was a Greek philosopher from over 2500 years ago who made many significant scientific and mathematical discoveries. Pythagoras’ Theorem was one of them. While this theorem is an important rule, remember that it only applies to right-angled triangles. Pythagoras’s Theorem states, “the square on the hypotenuse is equal to the sum of the squares on the other two sides." But what does that mean in practice?
Here’s a visual to help.
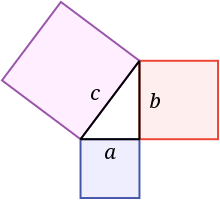
In the example, you can see that there are three squares. Each square has one side that, together with one side from each of the two other squares, forms a triangle between them. So, if the square of the hypotenuse is equal to the sum of the squares of the other two sides, then in a formula, that can be represented as a2 + b2 = c2. That’s Pythagoras’ Theorem!
In practice, this theorem means that you can use the length of any two sides on a right triangle to calculate the length of the remaining side. Remember that although a and b may be used interchangeably, the c designation in this equation always refers to the triangle’s hypotenuse.
The Three Basic Functions in Trigonometry
When beginning your studies, it’s essential to learn trigonometry’s three basic functions: sine, cosine, and tangent, often shortened to sin, cos, and tan, respectively. Simply put, each of these functions is an equation in which one side of a right-angled triangle is divided by another.
Remember that Greek letter theta (θ) that represents another angle in the triangle? For any angle θ, the
Sin θ = opposite / hypotenuse
Cos θ = adjacent / hypotenuse
Tan θ = opposite / adjacent
You might find it helpful to remember the abbreviations SOH, CAH, and TOA. If that’s still not easy enough to remember, you could create a funny mnemonic to help you, like "The Old Archaeologist Sat On His Coat And Hat.
Because of the relationships between the functions, Tan θ can also be calculated as Sin θ / Cos θ. That also means that:
Sin θ = Cos θ × Tan θ and
Cos θ = Sin θ / Tan θ.
Take the Math Tutor Matching Quiz to Find the Best Trigonometry Tutor
How Can Trigonometry Be Used With Circles?
The trigonometric functions you just read apply to triangles with right angles but can actually be applied to all angles, from 0 to 360°.
Angles can be measured or described in both degrees and radians.
A right angle is 90° and π/2 radians.
A straight angle is 190° and π radians.
A full rotation is 360° and 2π radians.
To convert radians to degrees, multiply by 180 and then divide by pi. To convert degrees to radians, multiply by pi and divide by 180.
To understand the use of trigonometry with non-right triangles, think about a unit circle (a circle with a radius of 1) and then divide it into four quadrants. The circle’s center is referred to as having a Cartesian coordinate of (0,0), meaning that its x value and its y value are both 0. Anything to the left of the center will have an x value of less than 0 (negative), and anything to the right will be more than 0 (positive). The same goes for the y values.
Because the circle has a radius of 1, we can measure sin, cos, and tan directly.
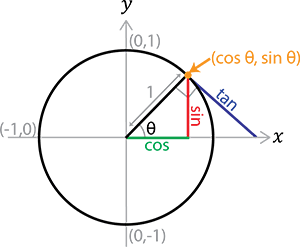
One of trigonometry’s lesser-known facts is that sine and cosine are percentages. These percentages vary from +100% to –100%, or the maximum positive to the maximum negative, since they are in a circle and can only extend to meet those parameters.
Graphs of Sine, Cosine, and Tangent
Sine, cosine, and tangent can all be represented graphically as well. If you were to plot the sine and cosine functions, you’d see this:
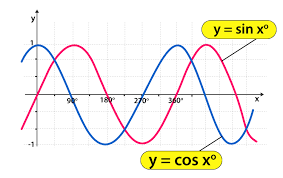
On a graph, the sine function goes up and down and has a curve that repeats every 2π radians (or 360°). It starts at 0, increases to 1, then goes down to –1.
Cosine is very similar, but it starts at 1 instead of 0, goes down to π radians (or 180°), and then heads up again.
The graph of the tangent function is very different.
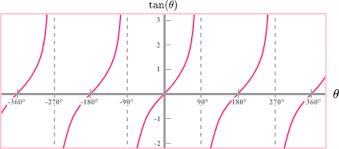
As you can see, the graphical representation of a tangent function goes between negative and positive infinity and crosses through 0 at every π radians (or 180°).
Find the Right Tutor to Make Trigonometry Easier
Although it may seem daunting now, trigonometry contains a wealth of interesting discoveries and ideas! Even so, we understand that trigonometry is a complex and challenging subject to navigate without help—which is where a tutor might help.
As you begin your search, remember that there are many things to consider when looking for a tutor. The right tutor for you will have qualities such as
- A deep understanding of trigonometry: The study of trigonometry inevitably brings up questions, and you’ll need someone who is able to give you a proper answer and explanation for all of them.
- Patience: As you wrestle with trigonometry, it may require time for you to get things right. The right tutor has the patience to move at your pace, explain concepts as many times as you need, and is willing to try different tutoring methods if something isn’t working.
- A teaching style that suits your learning style: While tutors should be flexible, every tutor has their own unique teaching style, just as you have a unique learning style. These styles should be compatible to ensure the best results.
- Great communication: Your tutor may have all the experience in the world, but it won’t mean anything if they can’t effectively communicate with you! Great communication also covers listening; if your tutor isn’t a good listener, you might need to keep searching.
- Extensive experience: An experienced tutor is equipped to handle any problems that arise and knows how to work best with different kinds of students.
- Diverse practice problems: Without practice, you will never master math. It’s important that your tutors recognize this and provide opportunities to practice without overwhelming you.
Conversely, there are some potential red flags to remember while researching tutors. Watch out for tutors who:
- Are impatient
- Don't have the right credentials or experience
- Are unreliable
- Have bad reviews
- Don’t provide enough examples or practice questions
How Learner Can Help You Master Trigonometry
Because Learner offers tutoring services online, students of all ages, locations, and backgrounds can find flexible, high-quality help. With online scheduling and a broad selection of tutors, students can meet with their tutors from the comfort of their own homes without worrying about travel time or geographical restraints. Additionally, Learner’s platform offers top-notch instruction at lower rates than many in-person competitors.
Take the Math Tutor Matching Quiz to Find the Best Trigonometry Tutor