Math can be divided into two broad categories: the rational and the irrational. Irrational numbers can't be broken down into fractions. Rational numbers, on the other hand, can be.
Pi is perhaps the best-known example of an irrational number. It's impossible to write down pi as a fraction, and it never ends or repeats in decimal form. This might seem like a minor distinction, but it's actually quite important!
Let’s define what an irrational number is and explore what sets irrational numbers apart from their rational counterparts and why they're so intriguing to mathematicians. Stay tuned for more on this fascinating topic!
What is an irrational number?
An irrational number is a real number that can't be written as a fraction or as the ratio of two integers. It is an infinite, non-repeating decimal that never ends and doesn't have a pattern.
Irrational numbers cannot be calculated exactly and must be approximated to solve mathematical problems. Examples of irrational numbers include π (pi), √2, and e, or Euler's number.
These numbers are not the same as their rational equivalents, which can be written as a fraction. Rational numbers are any number that can be written in the form a/b, where a and b are integers (whole numbers) with no common factors other than 1.
Examples of irrational numbers
Irrational numbers are essentially non-repeating, non-terminating decimals that cannot be represented as a fraction. Some examples include pi (3.14159...), the square root of two (1.414213...), and the golden ratio (1.618033...).
While irrational numbers can be used to describe nature's measurements, they can also demonstrate relationships between different objects or between an object and its environment.
For instance, in architecture, the Fibonacci sequence is often used to identify aesthetically pleasing proportions that demonstrate an irrational number, such as 1.61803... coinciding with the golden ratio's absolute mathematical precision.
Euler's number, denoted as e (2.71828...), is an irrational number that appears in many areas of mathematics and physics, such as exponential growth or decay, compound interest, and the number of possible configurations of a system.
As you can see, irrational numbers are not only used for calculations but also to create visually pleasing shapes and proportions. This is why they are so fascinating—they can be applied in a variety of fields and help us understand the universe in its entirety.
Why are they called "irrational"
Irrational numbers, or numbers that cannot be expressed as simple fractions, have earned the title "irrational" due to their inability to be represented in their simplest form.
While a fraction can represent a perfectly rational number like 1/2, certain other numbers, such as, are considered irrational because they are infinitely long and cannot be written exactly in fractional form.
Because of this, irrational numbers have an infinite number of digits after the decimal place, which makes them hard to work with or use in math.
For example, the number pi, denoted by the Greek letter π, is an irrational number often used in geometry. Pi is about 3.14159, and it is written as an endless string of digits that don't repeat after the decimal point. So, pi will always be an "irrational" number because it can never be written exactly as a simple fraction.
In math, there are many ways to get close to irrational numbers and work with them to make calculations easier. Depending on the situation and how accurate the answer needs to be, these methods can range from series expansions to numerical approximations.
How are irrational numbers used in math?
Irrational numbers are used in mathematics to describe a variety of concepts, and they appear in almost all areas of the subject. In algebra, irrational numbers can be used to solve equations or calculate the area of certain shapes.
In calculus, irrational numbers are useful for calculating limits and derivatives. They also appear in geometry and trigonometry when computing distances, angles, and areas.
In addition, irrational numbers appear in the study of probability and statistics. They can be used to calculate probabilities or model random phenomena like Brownian motion. Finally, they are important for solving equations that have no solution in rational numbers. By expressing the solution in irrational numbers, the equation can be solved analytically.
Overall, irrational numbers are a fundamental part of mathematics and can be used to solve many types of problems. They can appear in almost any mathematical field and can help us answer questions about the world around us.
Whether you're studying engineering, economics, or physics, irrational numbers are a key part of understanding how complicated the universe is.
How to calculate irrational numbers
One of the most common ways to calculate irrational numbers is through series expansions. A series expansion involves expressing a number as a sum of terms, with each term representing a fractional part of the whole number. For instance, in order to compute pi, one might use the following formula:
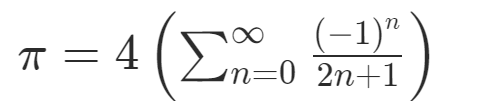
This formula is an example of a Taylor series, which can be used to calculate values for many different irrational numbers. Some numerical approximations, like the bisection method and Newton-Raphson iteration, can also be used to figure out irrational numbers.
In addition to numbers, geometric ideas like the Pythagorean Theorem and the golden ratio can be used to calculate irrational numbers. These geometric methods are great for figuring out values that depend on shapes, angles, and other geometric properties.
For example, the area of a circle is equal to pi multiplied by the square of its radius, and pi is an irrational number. The golden ratio can also be used to calculate the lengths of the sides of a regular pentagon or other similar shapes.
Finally, irrational numbers can also be calculated using algebraic methods. Finding the x-intercepts of an algebraic equation, like a quadratic equation, is a common way to figure out the value of an irrational number. The x-intercepts are then used to figure out the value of the irrational number.
Algebra is also used to solve equations with multiple variables, such as solving for a missing side in a triangle or calculating the circumference of a circle.
Real-world examples of the use of irrational numbers
A real-world example of irrational numbers is the measurement of the circumference of a circle. The formula for finding the circumference of a circle needs an irrational number, pi (π).
Pi is an irrational number with an infinite number of digits that never repeat and can’t be expressed as a fraction or decimal, making it impossible to measure the circumference of a circle without using pi.
The formula for finding the circumference of a circle is 2πr, where r is the radius of the circle. To calculate this, you must use pi to get an accurate answer. By knowing how to use irrational numbers in solving mathematical equations and problems, we can gain insight into their real-world applications.
For example, pi is used in engineering to calculate the circumference of a wheel, or to measure the distance around a track or field. In architecture, pi can help us calculate the size of columns and beams that are being used to construct buildings. Pi is also used a lot in physics, for example to figure out how planets move and where they go.
In addition to engineering and architecture, pi can be found in nature. For example, the relationship between a flower's petals and its center is based on pi. In biology, DNA strands have been observed to follow a pattern related to pi.
Understanding irrational numbers (with a little help)
The concept of irrational numbers can be a little difficult to grasp, but with a little bit of expert guidance, understanding numbers such as pi can become easier.
With Learner's expert math tutors, students can connect with a tutor with the knowledge and expertise to help them better understand irrational numbers such as pi. Our tutors know how to help students who are having trouble understand difficult ideas better.
At Learner, we believe that learning should be an enjoyable experience, and our math tutors strive to make the process as interactive and engaging as possible. With their help and expert knowledge, students will learn more about irrational numbers and be able to use what they've learned in different areas of math.
Our math tutors can help with more than just understanding irrational numbers. They can also help with things like problem-solving techniques, algebra, geometry, and even more advanced topics like calculus and trigonometry. This ensures that students receive the most comprehensive learning experience available.
Contact us today to learn more about how they can help you understand and excel with irrational numbers. Our experienced team will work diligently to ensure that you achieve your goals. We look forward to helping you succeed!