Put in the most simple terms, calculus is the study of rates of change. Calculus is one of many mathematics classes taught in high school and college. Calculus tutors can often help with concepts in calculus that students struggle to grasp. Calculus can be especially challenging because it involves concepts from algebra and geometry, as well as some trigonometry. This branch of mathematics originates from describing the basic physical properties of our universe, such as planetary motion and molecules.
Calculus approaches the paths of objects in motion as curves, or functions, and then determines the value of these functions to calculate their rate of change, area, or volume. Read on to learn more about what calculus is, where it originated, and the best way for students to succeed in calculus.
Who Invented Calculus?
Many students complete calculus problems without considering the history of the subject. The word "calculus" derives from words like "calculation" or "calculate," which have Latin origins. Many scholars have studied the origins of calculus, debated whether it was invented or discovered, and conducted research on who first used it.
Generally, math historians agree that calculus was independently discovered by Sir Isaac Newton and Gottfried Leibniz in the late 17th century. Newton’s interest in gravity and laws of motion led him to his breakthrough with calculus, while Leibniz focused mainly on consolidating calculus into one system. While both men are now given credit for their work on calculus, this was not always the case.
Calculus Controversy
In the late 1600s, English mathematician and physicist Sir Isaac Newton and German polymath Gottfried Leibniz simultaneously, yet separately, described how calculus could help solve problems in physics. Because the two men worked separately, controversy has long surrounded the true origins of the discovery of calculus. Leibniz published his work first, but Newton’s supporters accused Leibniz of plagiarizing Newton’s ideas, which were still unpublished at the time. In the early 18th century, the Royal Society in England – led by Newton – claimed that Leibniz had hidden his knowledge of Newton’s work. Eventually, this accusation was found to be false, though the controversy continued even after Leibniz died in 1716.
Today, the general consensus is that both men independently contributed to the invention and discovery of calculus. But even before these two great mathematicians discovered calculus, the ancient Greeks also made discoveries related to modern-day calculus. Despite the uncertainty surrounding the precise origins of calculus, the subject has continued to evolve and develop into what is studied in classrooms today.
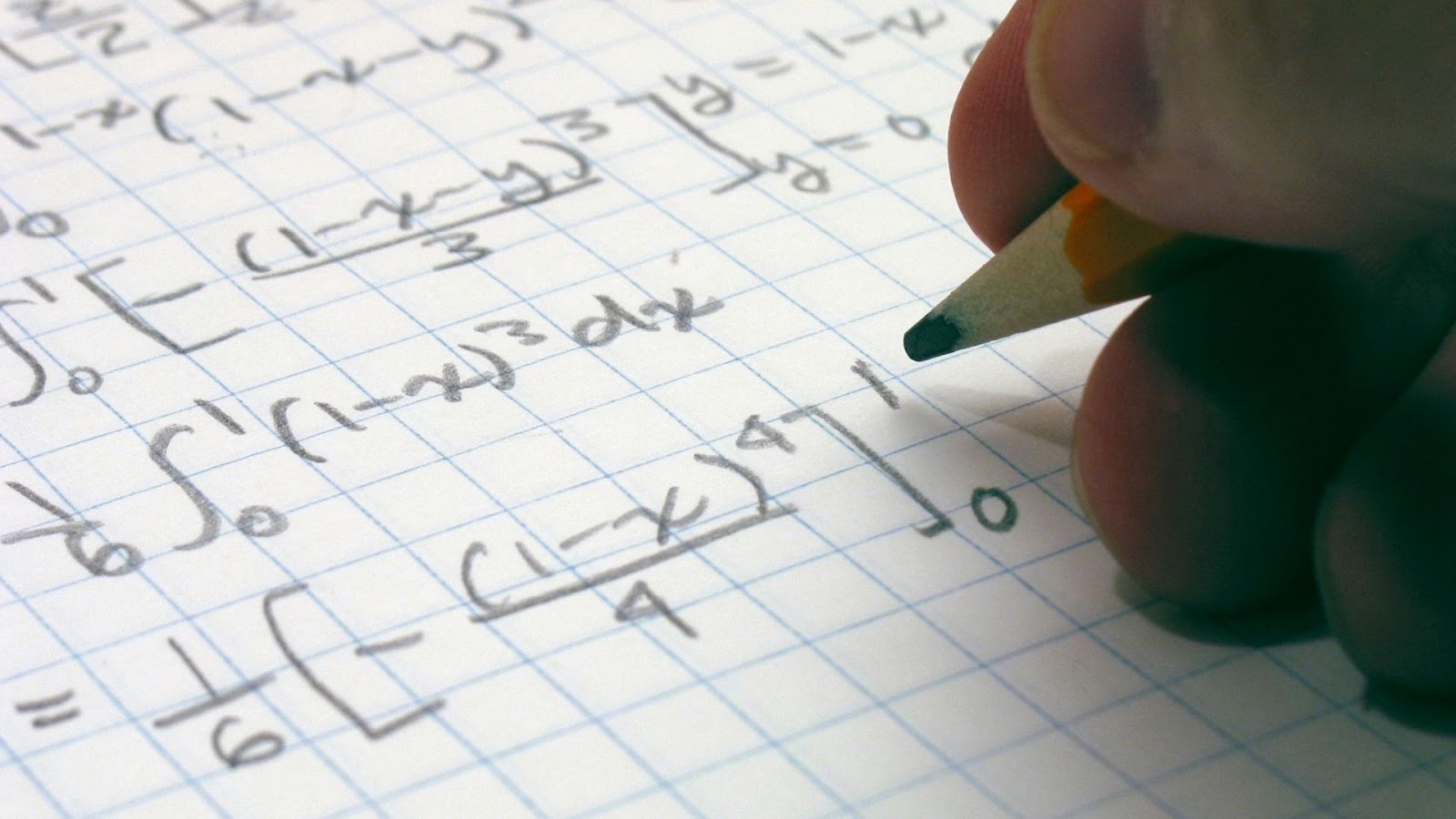
The Two Divisions of Calculus
The fundamental theorem of calculus establishes the two divisions of calculus: differential and integral. The two forms of calculus can be used to solve practical problems like the velocity of a moving object at a certain moment in time, or the surface area of a complex object, such as a lampshade. Calculus can also be used to gain a firmer understanding of the nature of space, time, and motion.
Differential Calculus
Differential calculus is usually taught before integral calculus. Differential calculus focuses on the rate of change of a quantity. It is concerned with the determination, properties, and application of derivatives and differentials. Differential calculus is used to find out the rate of change of a variable compared to another variable by using functions. Essentially, it helps people find out how a shape changes from one point to the next without dividing the shape into pieces.
Differential calculus describes the methods by which, given a function, you can find its associated rate of change function, called the "derivative." The function must describe a constantly changing system, such as the temperature variation over the course of the day or the velocity of a planet around a star over the course of one rotation. The derivatives of those functions would give you the rate that the temperature changed and the acceleration of the planet, respectively.
Integral Calculus
Integral calculus helps people to calculate the integral of a function. Integral calculus includes computations involving area, volume, arc length, center of mass, work, and pressure. One common use of this form of calculus is to find the definite integral of a function, which is the difference between the upper and lower values of the integral of a given function f(x).
Integral calculus can be thought of as the opposite of differential calculus. Given the rate of change in a system, you can find the given values that describe the system's input. In other words, given the derivative, e.g., acceleration, you can use integration to find the original function, e.g., velocity. Integration can also be used to calculate values such as the area under a curve or the volume of a solid.
This is possible since you begin by approximating the area with a series of rectangles, and then make your approximation more and more accurate by studying the limit. The limit, or the number approached by the approximations, will give you the precise area.
What Is the Fundamental Theorem of Calculus?
The fundamental theorem of calculus establishes the relationship between differentiation and integration. This gives people a way to evaluate definite integrals without needing to use Riemann sums or calculate areas. All of calculus relies on the fundamental principle that you can always use approximations of increasing accuracy to find the exact answer. For instance, you can approximate a curve with a series of straight lines: the shorter the lines, the closer they are to resembling a curve.
You can also approximate a spherical solid with a series of cubes that get smaller and smaller with each iteration and that fit inside the sphere. Using calculus, you can determine that the approximations tend toward the precise end result, known as the limit, until you have accurately described and reproduced the curve, surface, or solid.
How to Find Critical Points in Calculus
Students learning calculus should also be familiar with the process of finding the critical points of a function. Critical points are places where the derivative of a function is zero or undefined. Critical points are defined only in the domain of the derivative. When calculating critical points, students first need to calculate the derivative of the function. Then, they need to set that derivative equal to 0 and solve for x. Each x value that is found is known as a critical number. Students can then plug each critical number into the original equation to determine the y values. The related term “critical value” refers to the value of the function at the critical points.
What Does Differentiable Mean in Calculus?
Differentiability is another concept that is relevant to the application of calculus. Functions can be differentiable or non-differentiable. When a function is differentiable, there is a defined derivative at a specific point. This means that the slope of the tangent line of the points from one side is approaching the same value as the slope of the tangent of the points from the other side. Thus, a function is said to be differentiable if the derivative of the function exists at every point in its given domain. If the derivative does not exist at any one point in its domain, the function is said to be non-differentiable.
What Is a Variable in Calculus?
Students studying calculus (and other branches of mathematics) should be familiar with what variables are. In math, a variable is a quantity that may change within the context of a mathematical problem or experiment. Typically, a single letter is used to represent a variable. Commonly used letters include x, y, and z. X and y frequently represent real-number unknowns whereas z often represents complex-number unknowns. A function with a single variable is said to be univariate, a function with two variables is said to be bivariate, and a function with two or more variables is said to be multivariate.
What Is Multivariable Calculus?
Very few high schools include multivariable calculus in their mathematics curriculum. Multivariable calculus is more likely to be taught at the college level, and is most likely to be studied by mathematics majors.
Multivariable calculus is the extension of calculus to functions of several variables, including the differentiation and integration of functions involving multiple variables, whereas single variable calculus deals with the function of just one variable.
Where to Use Calculus
There are many professions and career paths that involve calculus, including engineering, medicine, biological research, statistics, pharmacology, space science, architecture, economics, and more.
Engineers
Engineers use calculus in a number of ways. Engineers make use of differential equations, linear algebra, and unknown variables in functions. Many different types of engineers use calculus, including mechanical engineers, aerospace engineers, structural engineers, and civil engineers.
Medicine
Calculus plays an important role in many aspects of the medical field. This branch of mathematics can be used to measure blood flow, cardiac output, and tumor growth. It’s also useful for studying topics such as population genetics.
Pharmacology
Calculus is used in pharmacology to determine dissolution rates for drugs and to calculate proper dosage. It’s essential to know the dissolution rates because drugs that dissolve too quickly can be toxic for the person taking them. Conversely, a drug that dissolves too slowly may not be effective. Thus, the correct dosage needs to be well defined for both safety reasons and effectiveness.
Biological Research
Biological research utilizes calculus in relation to several different yet important aspects of the life sciences. For example, calculus is used to determine growth and decay problems in organism populations as well as to study gene regulation and dynamic changes in biological events. Calculus can also be used to determine birth and death rates when considering a total population.
Statistics
Calculus is used in statistics with varying levels of difficulty. At the most basic level, calculus in statistics involves integrating over sections of a probability distribution. This will show the cumulative probability over those values.
Space Science
For a rocket to be sent into space, scientists must use calculus to figure out how much fuel the rocket needs to reach the correct velocity to break through the atmosphere. This math can also be used to calculate planetary motion. Calculus is used in space science alongside other core subjects, including physics.
Architecture
Architects regularly use math in their everyday roles, and calculus is essential to the duties of an architect. Calculus is used to determine how much material they need to complete a specific project and which types of support systems will prevent structures from collapsing.
Economics
In economics, calculus is used to study and record complete information, especially on graphs and curves. Calculus is frequently used to study supply and demand curves.
As you can see, calculus is essential to many different careers. It’s important that students do their best to understand calculus in case they decide to pursue a career that uses basic calculus concepts, or even more complex ones, such as multivariable calculus. This may lead parents and students to wonder: What is the best way to learn calculus?
Can You Learn Calculus Online?
There are many different types of learners – some thrive in in-person classes, while others excel in online settings. Thankfully, there are now education platforms that help students learn online as never before. Screen-sharing allows teachers, instructors, and tutors to show students step-by-step instructions on how to solve math problems. Teachers and tutors can easily pull up online visuals and other teaching aids with minimal effort. Calculus is well suited to being adapted to an online classroom setting so that students can learn from the comfort of their homes, if needed.
Even if they attend in-person classes for their primary instruction, many students rely on online math tutors to help them grasp challenging mathematical concepts – especially in a subject as difficult as calculus. Connecting with an experienced math tutor is one way to give high school and college students the best possible chance to learn difficult concepts across various mathematical disciplines.
How Learner Calculus Tutors Can Help
Tutoring can be very helpful for students at any academic level. If a student struggles with a specific topic, such as analytical geometry or differential and integral calculus, a tutor can pinpoint the best way to move forward with learning without creating confusion. And if a student excels at certain topics, a tutor has the ability to challenge them and encourage growth and out-of-the-box thinking.
A tutor can give students strategies, like mathematical models and examples, that can help them learn how to apply new concepts, rather than just memorizing formulas or textbook passages. Teachers do extraordinary work, but for every teacher, there is a classroom full of students who could benefit from individualized attention. Tutors can offer specific help so that all students have the tools and support they need to succeed.
Many websites advertise online tutoring services, but some of these sites utilize teaching practices that aren’t necessarily best for every student. It can be difficult to find a service that fits a student’s specific needs. Learner is one example of a student-focused tutoring service. To get started with a tutor from Learner, parents answer questions about their child’s academic background and unique needs. Then, a call is scheduled with an Academic Coach to pinpoint learning goals and objectives. Lastly, Learner custom matches students with the right tutor and allows students to meet with their tutor for the first time.
Need help with calculus? Speak with our academic advisor to get started with one of our online calculus tutors today.
Frequently Asked Questions About Calculus
When Do Students Take Calculus?
Students usually take calculus during their senior year of high school or their freshman year of college, though this varies from place to place. Typically, high school freshmen take Algebra I, sophomores take geometry, juniors take trigonometry or Algebra II, and seniors take either precalculus or calculus.
This sample progression of math classes is for students on the main track, not the honors track. Students in honors classes could take algebra in eighth grade, geometry as a high school freshman, trigonometry as a sophomore, precalculus as a junior, and calculus as a senior. However, this can also vary from school district to school district and from state to state.
How Long Is the AP Calculus AB Exam?
The AP Calculus AB exam is roughly equivalent to a semester of college calculus. This exam has two sections, each with a Part A and a Part B. Students will encounter multiple choice questions in the first section and free response questions in the second section, with a total of three hours and 15 minutes allotted to complete the exam.
Do You Need Calculus for the SAT?
The SAT does not usually include calculus problems, but it's still a good idea for students to have a solid understanding of basic calculus concepts by the time they start college. Students are more likely to see math problems involving algebra, geometry, and basic trigonometry on the SAT.
Is Calculus Required for Medical School?
Many medical schools require at least a year of college-level mathematics, and they’ll often recommend that students take calculus or statistics. Getting in touch with an academic advisor linked to the program of interest is the best way to find out which math courses are required, as requirements can vary from state to state and program to program.
What Comes After Calculus?
Not only does calculus implement different math topics like geometry, trigonometry, and algebra, but calculus is also used as a building block for other higher-level math courses. After students complete Calculus I, they’ll often move on to Calculus II, Linear Algebra, or Differential Equations. Students may also take classes involving aspects of multivariable calculus. These courses are usually offered at the college level, as Calculus I is usually taken by high school seniors (or college freshmen).
How is Precalculus Different from Calculus?
Precalculus is a prerequisite to calculus. Calculus builds on concepts taught in precalculus, trigonometry, and other math subjects to solve various problems. Precalculus often involves a review of Algebra 2, concepts in trigonometry, parametric equations, and more.
Do You Need Precalculus to Learn Calculus?
In most public schools, precalculus is a required prerequisite to calculus, though some schools may allow students to take calculus even if they have not taken precalculus. Either way, precalculus is an excellent way to get acquainted with and practice concepts that will be reinforced in calculus.
Is Calculus Hard?
Although calculus (and other math subjects) may come easily to some, calculus is generally considered to be a difficult subject, and one that requires a significant amount of prior mathematical knowledge. There is a good reason why calculus is taught to high school seniors instead of high school freshmen. If a student decides to major in math, calculus is considered an introductory course to higher-level math courses in college.
Why Is Calculus Important?
Calculus is an extremely important part of everyday life. Calculus helps professionals understand the motion of astronomical equipment, weather patterns, the movement of sound and light, and electronic circuits and systems. So even if a student does not directly utilize calculus in their own life, there are many ways in which calculus is used in the professions surrounding them.
What Is a Dependent Variable?
Dependent variables are determined, or depend, on the values of other variables. Essentially, the dependent variable is the variable that is being measured or tested.
What Is the Derivative of a Function?
The derivative of a function is a fundamental tool in calculus. It measures the sensitivity to change of the output value with respect to the input value.
What Is Infinitesimal Calculus?
Infinitesimal calculus is the study of continuous change. Calculus was formerly known as infinitesimal calculus.